展开原理:利用体积不变的原则:用某一截面的总面积去除以材料厚度可得到该方向的展开长度,其实展开就是同一尺寸也因各人经验而羿,没有绝对的一个数值,只要在公差范围即可。
展开要点:步骤如下
1:看懂产品图,能想象出它的立体形状以及具体每一部位的细节(展开前的基本要求)
2:弄清楚产品的材厚和材质
3:具体展开计算
1):用体积法(一般适合有变薄的弯曲)
2):用展开计算公式
由于产品在弯曲过程中有的地方被拉长或压缩,但总可以找到某一层的弯曲线长度是不变的,这一不变的层叫中心层(不是中间层),我们就是利用中心层来进行展开的;因此,我们要想进行展开,就必须找出中心层。
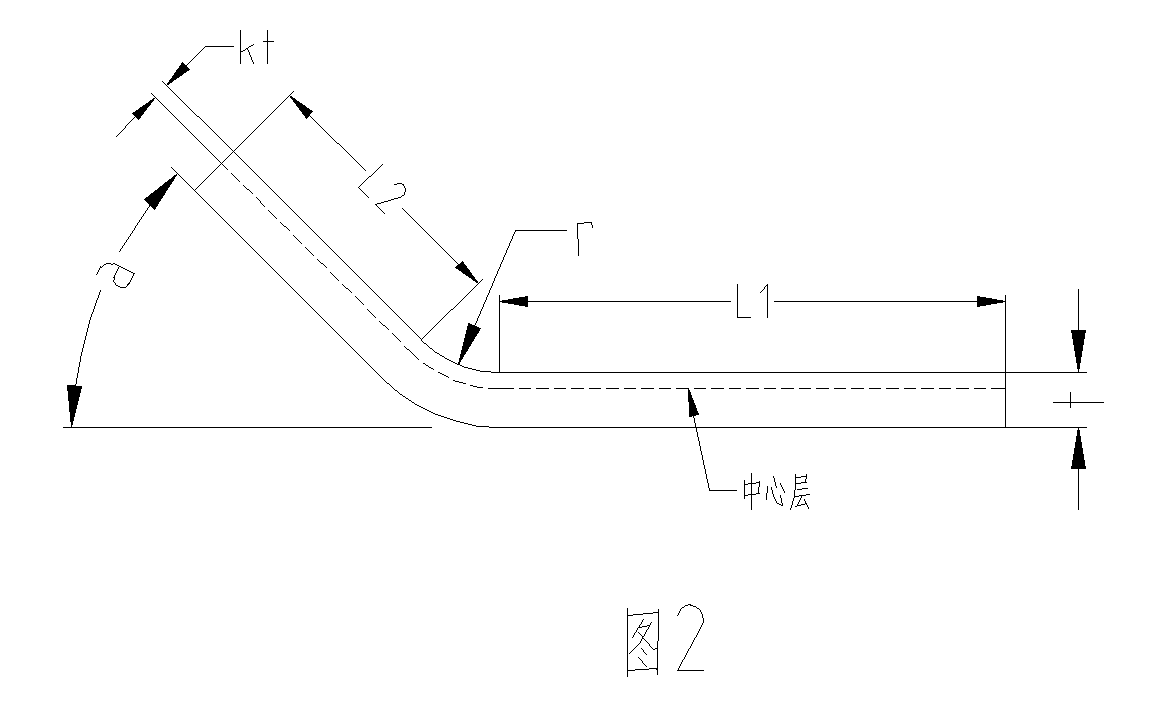
如图2,设中心层系数为K,弯曲内半径为r,材料厚度为t,弯曲角为a,L1,L2为直线部分长度,展开长度值为L
那么则有L=L1+L2+2π(r+kt)a/360
中心层系数K的大小根据实践经验可按下列公式选取
1):当r/t<=0.50时 k=0.25
2):当0.5<r/t<=1.0时 k=0.25~0.30
3):当1.0<r/t<=2时 k=0.30~0.33
4):当2.0<r/t<=4时 k=0.33~0.38
5):当r/t>4.0时 k=0.38~0.45
此公式适合一切材料厚度的弯曲展开计算,具体在实践应用中
当R/T取上限时,K也应取上限值,如当R/T=0.5时,K=0.30
当r/t=0~0.5时,即所谓的清角,此时k=0.25t~0.3t
若是90°清角弯曲时L=0.4~0.45t"的值是一样的,只不过后者是前者的一个特例,在此推算一下
L=2πK/4=2π*0.25t/4=πt/8=0.3925t=0.40t
L=2πK/4=2π*0.30t/4=πt/8=0.4710t=0.45t
也就是说当清角90°弯曲时用L=0.4t~0.45t或K=0.25~0.30t两个公式来展开计算都行
4:当包圆时,此时展开计算公式已和上面不一样,因为包圆时,材料厚度变薄很小,或者几乎不变,中性层接近中间层。
1):当包小圆时(∅D<5.0),其中心层系数K=0.45
2):当包圆时5.0<∅D<10.0)其中心层系数K=0.45~0.50
3):当包大圆时(∅D>10.0),其中心层系数K=0.5~0.55
5:通过查表,找出中心层系数的大小,再进行展开计算也行,在此不作详细叙述。
6:产品的圆角处理:产品上的圆角一般保持不变它,但若是尖角,一般用最小圆角R0.13去拟化它,对于产品上R0.1的圆角,尽量用R0.13去代替;对于R<0.1的圆角或清角,如果是重要尺寸(改变会影响功能)则不变它,採用过切来达到要求。
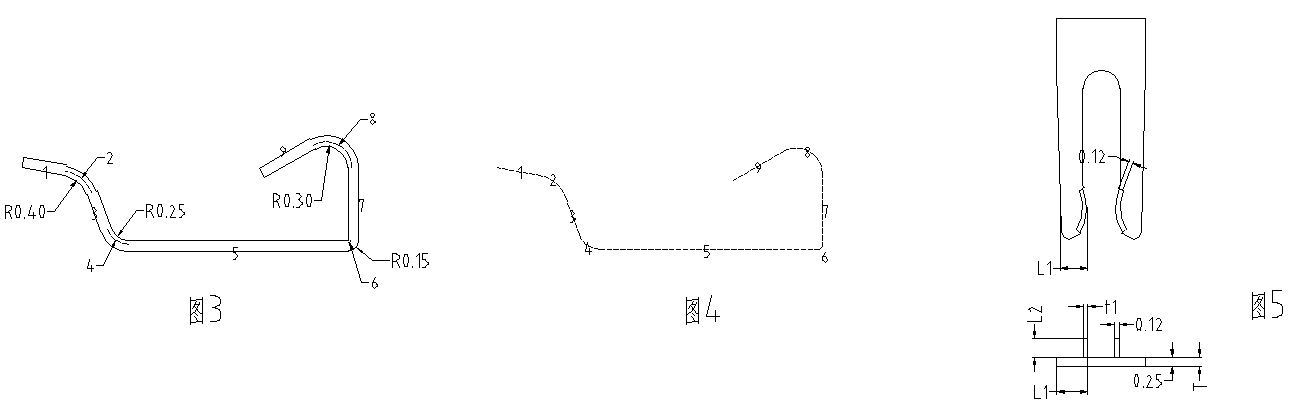
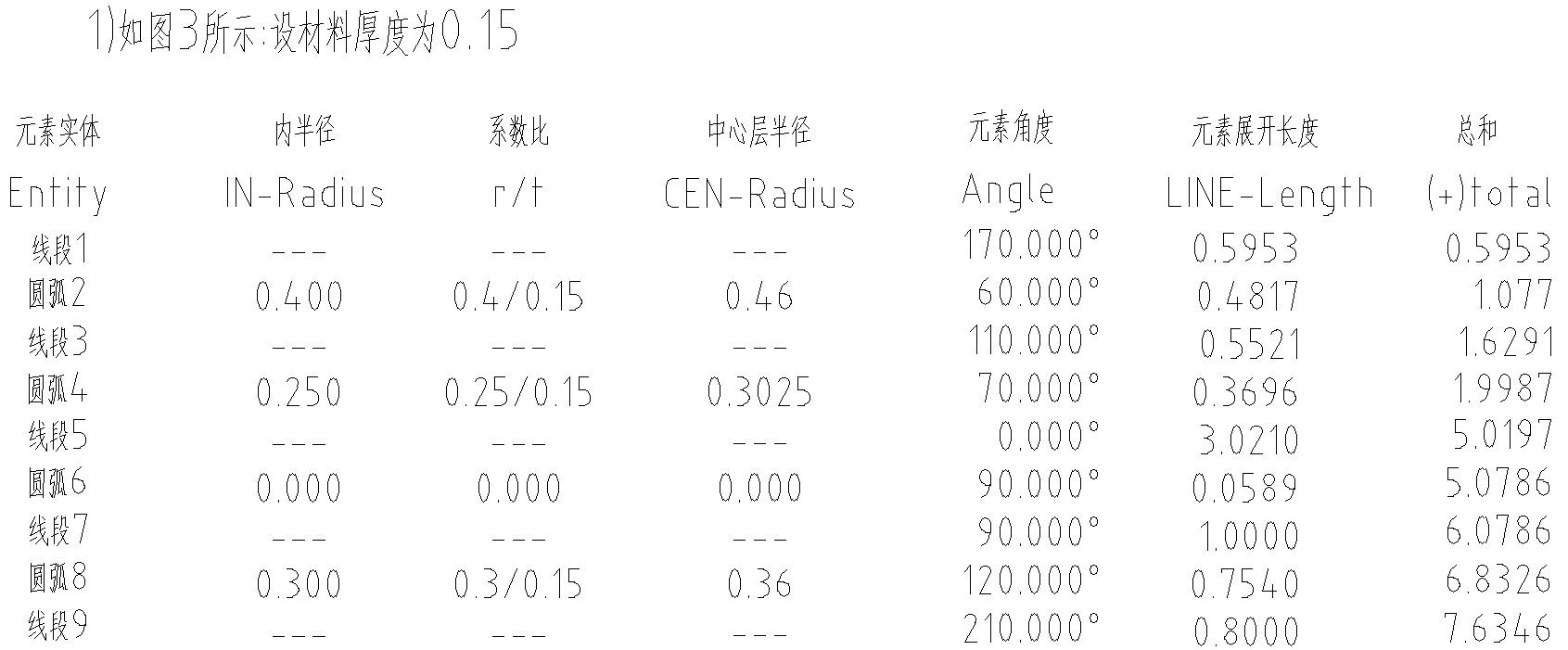
该图形的展开总长7.6346,取7.63,在展开时,直线部位可取材料厚度的任一边,(因为两者平行相等)在圆弧部分,必须是内r偏离一个kt距离,再用MO命令量出这个半径为r+kt的圆弧的长度,就是圆弧部分展开长度。
技巧:找出中心层后可把中心层各段直线圆弧首尾连接起来,再用PE命令把直线和圆弧编辑成一条多义线,再用 len命令量出这条多义线的长度(即展开总长):这样快一点,可以省畋一个个去相加如本例中:1.2.3;4.5;7.8.9可把这9条线段编辑成1条多义线,再量出长度即可得展开全长如图4
2)如图5所示:设材料厚度为0.25
从图中可以看出:向上弯曲的两个耳朵材料已经被挤薄了(0.12)那么在展开时,就只能按体积计算了
其展开长度L=L1+L2*t1/T








还没有评论,来说两句吧...